Altura en tres dimensiones
La altura de un objeto o figura geométrica es una longitud o una distancia, usualmente vertical o en la dirección de la gravedad. Este término también se usa para designar la coordenada vertical de la parte más elevada de un objeto. En coordenadas cartesianas (x, y, z), la altura de los volúmenes corresponde a la coordenada Z que es la que se sitúa perpendicular al suelo (vertical), normalmente, ya que X e Y son asignados a valores horizontales: anchura (o ancho) y longitud (o largo). Popularmente, el sustantivo «altura» puede ser reemplazado por «alto» (adjetivo sustantivizado), que la Real Academia Española acepta como vigesimotercera acepción en su Diccionario.1[editar] Altura en figuras planas
En figuras contenidas en el plano euclidiano, la altura es la distancia perpendicular a un eje horizontal fijado por convención. En coordenadas cartesianas (x, y), en el plano, la altura se refiere a la distancia perpendicular al eje X, o la longitud de un segmento paralelo al eje Y. En un paralelogramo, la altura es la menor distancia entre los dos lados paralelos.En un cuadrilátero con al menos dos lados paralelos, la altura es la menor distancia entre los dos lados paralelos.
[editar] Alturas de un triángulo
En un triángulo la altura respecto de un lado, es la distancia entre la recta que contiene al lado y el vértice opuesto. Equivale a un segmento perpendicular a dicho lado con un extremo en el vértice opuesto y el otro en dicho lado, o en su prolongación. La intersección de la altura y el lado opuesto se denomina «pie» de la altura.
La magnitud de la altura sirve para calcular el área de un triángulo, siendo su valor: a = b·h/2, donde a es el área, b la base –la longitud del lado "inferior"–, y h su altura correspondiente.
En la figura, pueden ser BC·AA"/2, AB·CC"/2 o AC·BB"/2.
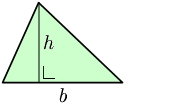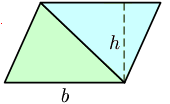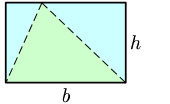
Ésta fórmula se puede demostrar, geométricamente, trazando un rectángulo cuya área es el doble del área del triángulo, con la misma base y la misma altura.
